Skip to content

第 328 场周赛

比赛链接

Date: 2023-01-15

A 数组元素和与数字和的绝对差

Python 快乐题

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
class Solution {
public:
    int differenceOfSum(vector<int>& nums) {
        int s = accumulate(nums.begin(), nums.end(), 0);
        int t = 0;
        for (auto x : nums) {
            for (auto c : to_string(x)) {
                t += c - '0';
            }
        }
        return abs(s - t);
    }
};

1
2
3
4
5
class Solution:
    def differenceOfSum(self, nums: List[int]) -> int:
        s = sum(nums)
        t = sum(sum(map(int, list(str(num)))) for num in nums)
        return abs(s - t)

复杂度分析

  • 时间复杂度：\(O(n)\)
  • 空间复杂度：\(O(1)\)

B 子矩阵元素加 1

二维前缀和，容斥原理

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    vector<vector<int>> rangeAddQueries(int n, vector<vector<int>>& queries) {
        vector<vector<int>> s(n, vector<int>(n));
        for (auto v : queries) {
            s[v[0]][v[1]]++;
            if (v[3] + 1 < n) s[v[0]][v[3] + 1]--;
            if (v[2] + 1 < n) s[v[2] + 1][v[1]]--;
            if (v[2] + 1 < n && v[3] + 1 < n) s[v[2] + 1][v[3] + 1]++;
        }
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                if (i > 0) s[i][j] += s[i - 1][j];
                if (j > 0) s[i][j] += s[i][j - 1];
                if (i > 0 && j > 0) s[i][j] -= s[i - 1][j - 1];
            }
        }
        return s;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution:
    def rangeAddQueries(self, n: int, queries: List[List[int]]) -> List[List[int]]:
        s = [[0] * n for _ in range(n)]
        for r1, c1, r2, c2 in queries:
            s[r1][c1] += 1
            if r2 + 1 < n:
                s[r2 + 1][c1] -= 1
            if c2 + 1 < n:
                s[r1][c2 + 1] -= 1
            if r2 + 1 < n and c2 + 1 < n:
                s[r2 + 1][c2 + 1] += 1

        for i in range(n):
            for j in range(n):
                if i > 0:
                    s[i][j] += s[i - 1][j]
                if j > 0:
                    s[i][j] += s[i][j - 1]
                if i > 0 and j > 0:
                    s[i][j] -= s[i - 1][j - 1]
        return s

复杂度分析

  • 时间复杂度：\(O(n^2)\)
  • 空间复杂度：\(O(n^2)\)

C 统计好子数组的数目

如果子数组 \([l, r]\) 是一个好子数组，那么对于所有的 \(r' \ge r\) , \([l, r']\) 都是好子数组。

所以，可以使用双指针（或者说是滑动窗口）来解决本题，对于每个 \(l\)，求出最小的 \(r\) 使得 \([l, r]\) 是好子数组即可。过程中维护一个哈希表，记录区间内每种数字出现的次数，动态的维护 \((i, j), i<j, \textit{arr}[i]=\textit{arr}[j]\) 的个数。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    using ll = long long;
    long long countGood(vector<int>& nums, int k) {
        ll res = 0;
        ll sum = 0;
        unordered_map<int, int> mp;
        auto update = [&](int x, int cnt) {
            sum -= 1ll * mp[x] * (mp[x] - 1) / 2;
            mp[x] += cnt;
            sum += 1ll * mp[x] * (mp[x] - 1) / 2;
        };
        for (int i = 0, j = 0; i < nums.size(); i++) {
            while (j < nums.size() && sum < k) {
                update(nums[j], 1);
                j++;
            }
            if (sum >= k) {
                res += nums.size() - j + 1;
            }
            update(nums[i], -1);
        }
        return res;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
class Solution:
    def isItPossible(self, word1: str, word2: str) -> bool:
        h1, h2 = Counter(word1), Counter(word2)
        l1, l2 = len(h1), len(h2)
        for x in h1:
            for y in h2:
                if x == y:
                    if l1 == l2:
                        return True
                    continue
                # 计算交换操作之后的种类数
                nl1 = l1 - 1 if h1[x] == 1 else l1
                nl2 = l2 - 1 if h2[y] == 1 else l2
                nl1 = nl1 + 1 if h1[y] == 0 else nl1
                nl2 = nl2 + 1 if h2[x] == 0 else nl2
                if nl1 == nl2:
                    return True
        return False

复杂度分析

  • 时间复杂度：\(O(n)\)
  • 空间复杂度：\(O(n)\)

D 最大价值和与最小价值和的差值

首先，树中最远的两点距离被称为树的直径。我们可以用两次 BFS 来求出它。

  1. 首先随便选一个点（比如 \(0\)）进行 BFS，结束后找到距离起点最远的点，把它设为 \(s\)。
  2. 然后从 \(s\) 开始 BFS，结束后找到距离 \(s\) 最远的点，把它设为 \(t\)。

此时，\(s\) 到 \(t\) 的距离就是树的直径，是整个树中两点配对距离最远的一对点。

但是最终的答案并不一定是以 \(s\) 或者 \(t\) 为根。例如下图中，\(1\) 到 \(5\) 是直径，但是答案是 \(7\) 到 \(5\)。

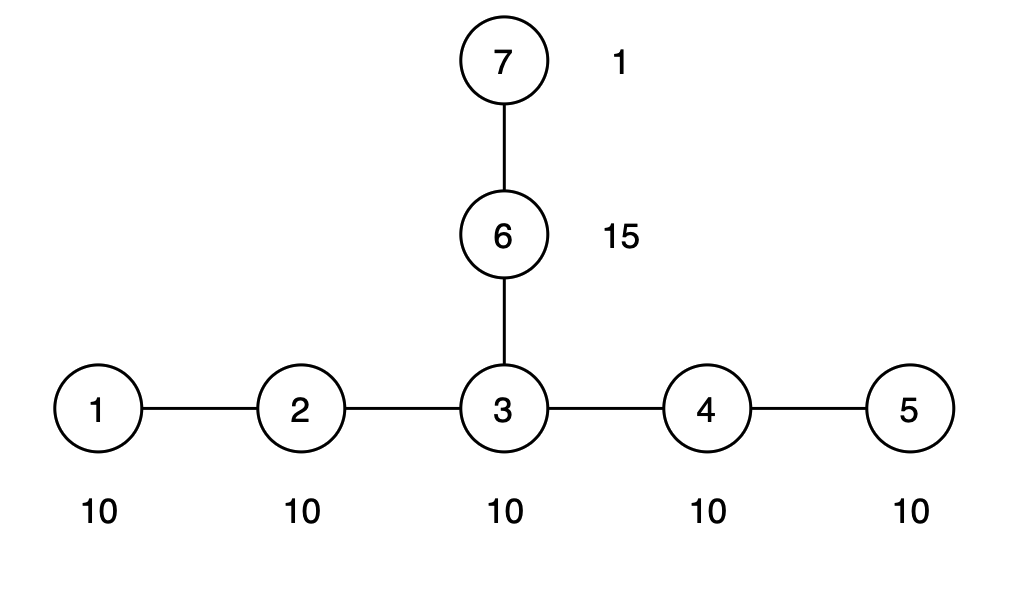
所以，我们应该求出从 \(s\) 以及从 \(t\) 出发到达所有点的距离。然后遍历所有点，枚举以它为根时的答案。这样做的正确性在于，在树中距离每个点最远的点不是 \(s\) 就一定是 \(t\)。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Solution {
public:
    using ll = long long;
    using PII = pair<int, int>;
    long long maxOutput(int n, vector<vector<int>>& edges, vector<int>& price) {
        vector<vector<int>> g(n);
        for (auto v : edges) {
            g[v[0]].push_back(v[1]);
            g[v[1]].push_back(v[0]);
        }
        vector<ll> ds(n), dt(n);
        auto bfs = [&](int s, vector<ll>& d) -> int {
            vector<ll> v(n);
            d[s] = price[s];
            queue<int> q;
            q.push(s);
            v[s] = 1;
            int rt = -1;
            while (q.size()) {
                auto x = q.front(); q.pop();
                if (rt == -1 || d[rt] < d[x]) {
                    rt = x;
                }
                for (auto y : g[x]) {
                    if (v[y]) continue;
                    d[y] = d[x] + price[y];
                    q.push(y);
                    v[y] = 1;
                }
            }
            return rt;
        };
        auto s = bfs(0, ds);
        auto t = bfs(s, ds);
        bfs(t, dt);
        ll res = 0;
        for (int i = 0; i < n; i++) {
            res = max(res, 1ll * max(ds[i], dt[i]) - 1ll * price[i]);
        }
        return res;
    }
};

复杂度分析

  • 时间复杂度：\(O(n)\)
  • 空间复杂度：\(O(n)\)
本站总访问量 Loading 次 本站总访客数 Loading 人